介绍一下最近在牛津数学系和Sarah Waters和Nick Trefethen教授做的一个流体计算的工作:Xue, Y., Waters, S. L. and Trefethen, L. N. 2024. Computation of two-dimensional Stokes flows via lightning and AAA rational approximation. SIAM Journal on Scientific Computing. 46(2), pp.A1214--A1234. 二维低速流体谈不上前沿(如果不搭配上传热传质生物化学工业应用的话),像Moffatt eddy, lubrication theory, Hele Shaw什么的很多重要工作上世纪中叶就做的差不多了。但问题是可以利用解析法或者各种近似法求解的二维斯托克斯方程(2D Stokes equations)是极其有限的,而大部分问题只能借助数值方法(FEM&BIM)。我们的这个工作基于有理近似最近几年的快速发展(比如Nick的AAA算法,顺带说一句Nick通过这个算法拿了去年在北京举办的第一届基础科学大会科学前沿奖,计算数学只给了两个,另一个是George Karniadakis的PINN),提供了一种对于一般低雷诺数二维流体的半解析求解方法,使得一般的二维Stokes流问题可以在一秒钟内得到至少六位数的精确度,也算是挑战了一下传统数值方法在流体领域的应用。我们正在把这个算法应用到更实际的生物、医学、工业、环境流体问题,后续还会有其他文章(也包括一些新算法的文章)。
1. Goursat方程
法国数学家Goursat早在1898年就提出了二维重调和方程(2D biharmonic equations)的解可以由两个复解析函数表示,这两个函数经常被称为Goursat方程。重调和方程在固体和流体力学中有很多应用,在固体力学对应二维材料的线性形变,而在流体力学中就对应的是二维低速流体问题。如果求解出了两个满足边界条件的在域内解析的Goursat方程(或者在一定误差范围内满足边界条件),那么就相当于求解了最初的流体问题。
尽管Goursat早在一百年前就提出了这个理论,但直到我们这篇文章发表之前,实际上并没有一个有效的方法具体算出一个一般问题的Goursat方程。比如剑桥的A. S. Fokas给出了一个Fokas方法(又叫Unified Transform Method),可以通过一些复域内的一些复杂积分和正交多项式(比如切比雪夫)来近似Goursat方程在边界的值。然后再通过沿边界的柯西积分方程来计算Goursat方程在计算域内的值。这个方法最大的局限主要是基本只能用于多边形区域的问题(至少边界要是个关于z的函数),而且极难计算。我花了三个月时间试验这个方法,但是没有成功的算出一个结果。因此,如何在一个给定的一般区域计算出Goursat方程的表达式是个困扰了大家很长时间的问题。
2. 解析函数的奇点和有理近似
求解Goursat方程的难点,在于他们在边界或边界附近的奇点。所谓奇点,大概可以理解为不连续或不可导的点,比如 的奇点就是
。而对于流体问题,最显而易见的奇点就是边界上的拐点,因为紧贴边界的流线在拐点附近要突然改变方向。因此如果要准确求解Goursat方程,用来近似拟合的方程也需要有同样的性质。但我们前面说过Goursat方程是复解析函数,而解析函数的性质就是不能有奇点(或者极点)。因此现在出现了一个矛盾,我们需要求解的最终结果(尽管我们还不知道这个结果是什么)在边界有奇点,而表示它的函数又不能在边界有奇点。这个问题其实也是导致前面所说的Fokas方法收敛很慢的原因,因为正交多项式并不适合拟合有奇点的问题。最简单的例子是用多项式拟合
或
。
而最近一系列有理近似方向的重要工作表明(Gopal & Trefethen, 2019, SINUM),只要使用另一个有理方程,其中这个有理方程有从外部指数型靠近被近似方程奇点的n个极点,那么就可以在边界获得小于 的误差,而对于多项式这个误差在
数量级。打个比方,如果用有16个极点的有理方程计算到了小数点后的第四位,那么只需要使用25个极点就可以算到第五位,36个就可以到第六位。而如果使用多项式用16项算了四位,那么则需要160项算五位,1600项算六位。这之间效率的对比是很惊人的。Nick把这个算法称作闪电算法(The Lightning Algorithm),一方面闪电代表这个算法的速度,另一方面闪电一般会打向建筑物的尖端,也形象的代表了需要向拐点聚集方程的极点。
 碎片大厦上的闪电(来源BBC)
碎片大厦上的闪电(来源BBC)牛津数学系的Pablo Brubeck和Nick Trefethen(Brubeck & Trefethen, 2022, SISC)应用闪电算法计算了多边形内的二维Stokes问题,大部分问题都在一秒内得到了10位左右准确的结果。比如在下图典型的方腔流体问题中,通过在四角外部指数型放置有理函数的极点(红色圆点),就可以快速得到区域内流场。其中左下角和右下角还画出了第一级需要数位精度的Moffatt涡流。有理近似方法除了不需要画网格外,还有一个优点就是得到Goursat方程后可以快速区域内任何一点的任何物理量,不需要插值近似。
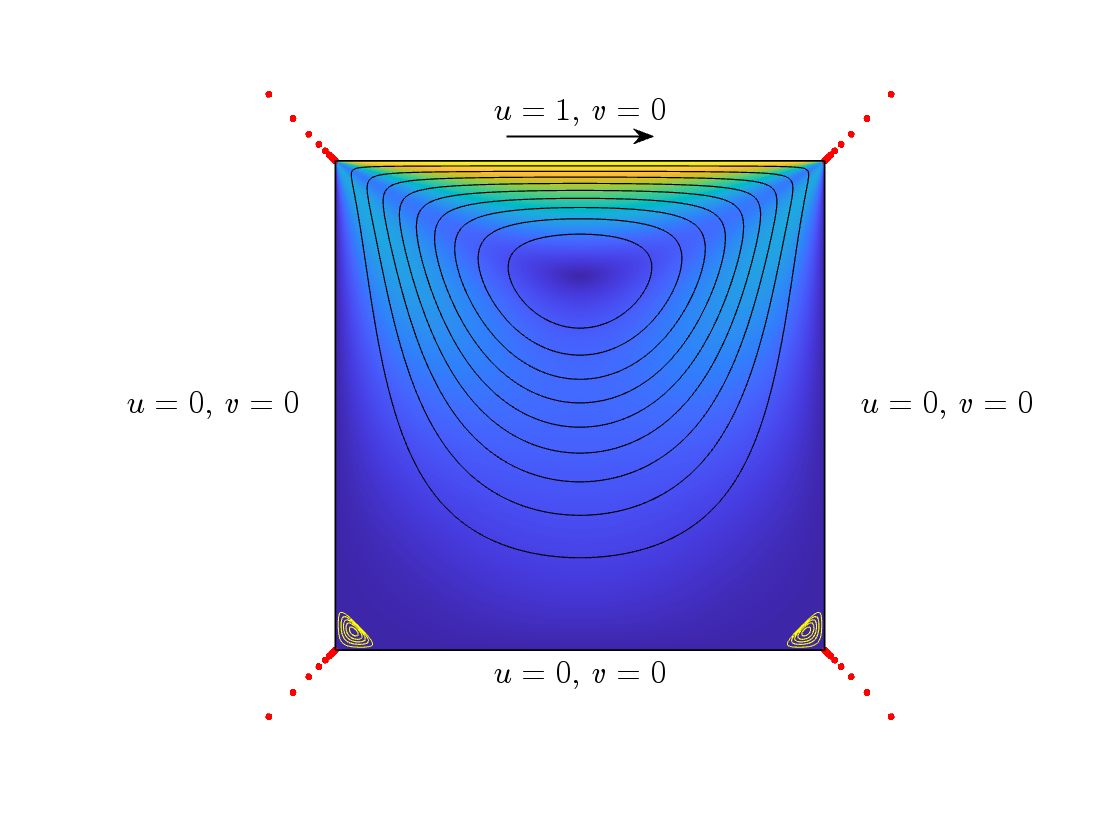 方腔内的Stokes流(Brubeck & Trefethen, 2022)
方腔内的Stokes流(Brubeck & Trefethen, 2022)3. LARS算法
闪电Stokes算法对于多边形内的二维低速流体问题都非常有效,但对于更一般的二维Stokes问题(比如边界是弧线,再比如内部有其他的几何体)则需要一些其他的有理近似算法才能解决。一个比较经典的问题是普林斯顿Howard Stone组用Extended Lubrication Theory (ELT)解决过的一个收缩管道问题(Tavakol et al., 2017, Proc R Soc A)。在这个问题中需要考虑一段弧线边界,其中最窄部分的上边界有非常大的曲率。这个问题尽管没有边界上的奇点,但在上边界很近的地方存在奇点(当收缩比例比较大的时候),这个时候用多项式近似也不能得到很好的收敛。但这个问题的难点是,尽管我们知道应该在一些边界外靠近奇点的位置放置有理函数的极点,但是并不知道这些极点的位置。所以这个问题的难点是当我们拟合一个一般边界上的函数时,如何找到边界附近极点的位置。
这时就要用到上文提到的AAA算法了(Nakatsukasa, Sète & Trefethen, 2018, SISC)。AAA算法可以自动寻找在一个边界上近似一个函数的最佳(或者接近最佳)的有理函数。当然在求解Goursat方程的问题中,我们不需要这个有理函数(因为不同于一般的Laplace问题,我们有两个Goursat方程,而我们只知道由它们共同决定的边界条件),但我们需要这个有理函数提供的极点。简单来说就是我们先沿问题边界近似Schwarz方程( )得到极点,再用在计算域外的极点组成的基来计算代表Goursat方程的有理函数(Costa & Trefethen, 2023)。我们选择Schwarz方程是因为这个方程只取决于边界的几何,而不取决于边界的函数值(这个方程就是把原方程沿着x轴反转了一下)。其实这个做法是比较大胆的,因为第一,Schwarz方程并不是我们最终要近似的方程,而第二,我们扔掉了区域内的极点(因为Goursat方程需要在区域内解析)。我们现在只能说这个算法有效,但还没有对它为什么有效的理论证明(最新的成果是Nick刚发表的一篇预印)。
另一个改进是我们可以用Laurent级数来考虑多联通区域,这其实是个流体领域内很重要的一类问题,比如疏松介质、颗粒运输、微流控等等。但是基于Harmonic Conjugate Theorem (Axler, 1986, Am Math Mon),对于每一个区域内的洞,除了Laurent级数我们还需要对两个Goursat方程各添加一个log的自由度,来保证物理量不会有多个解。对于用Laurent级数解决二维Stokes流问题,我们不是第一个,比如 Price, Mullin & Kobine (2003, Proc R Soc A)。
但我们发现只要把上述的三个算法结合起来,再对于这些基底进行正交化,就可以计算一般区域内的Goursat方程,从而解决一般的二维Stokes流体问题。这也就是LARS算法(Lightning-AAA Rational Stokes,原谅这个有点中二的北欧名字)。下面给大家放几个算例,代码可以从GitHub下载:https://github.com/YidanXue/LARS
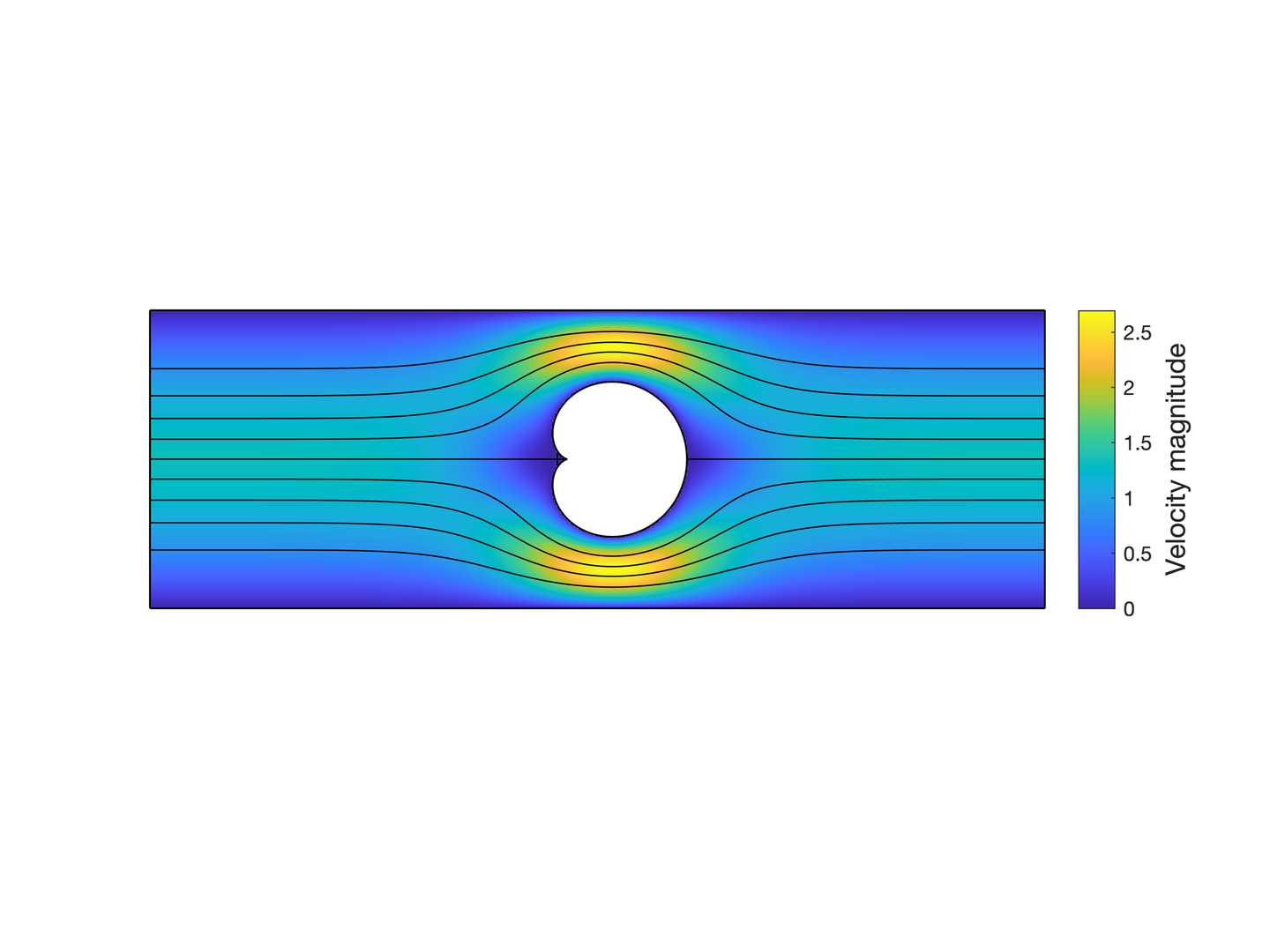 看似只是一个简单的圆柱绕流问题
看似只是一个简单的圆柱绕流问题 而如果我们放大新型孔洞左侧的区域,可以看到数个Moffatt涡旋
而如果我们放大新型孔洞左侧的区域,可以看到数个Moffatt涡旋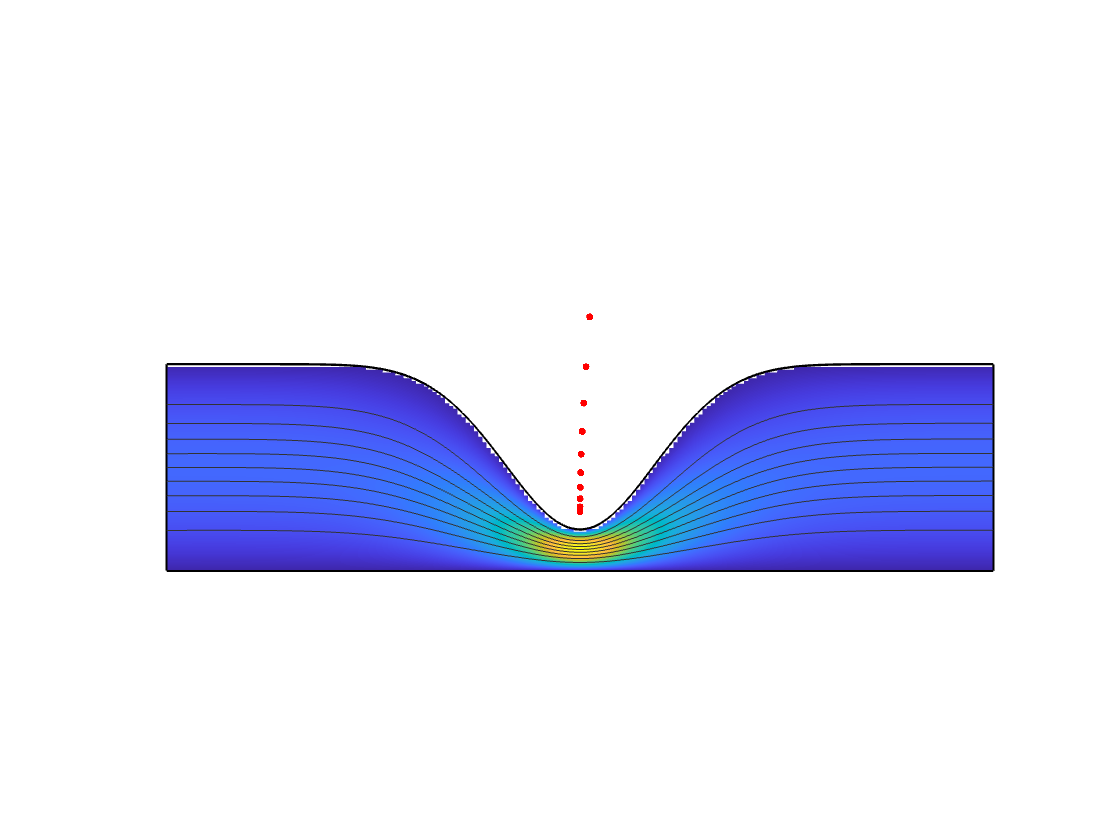 和Nick做的一个demo
和Nick做的一个demo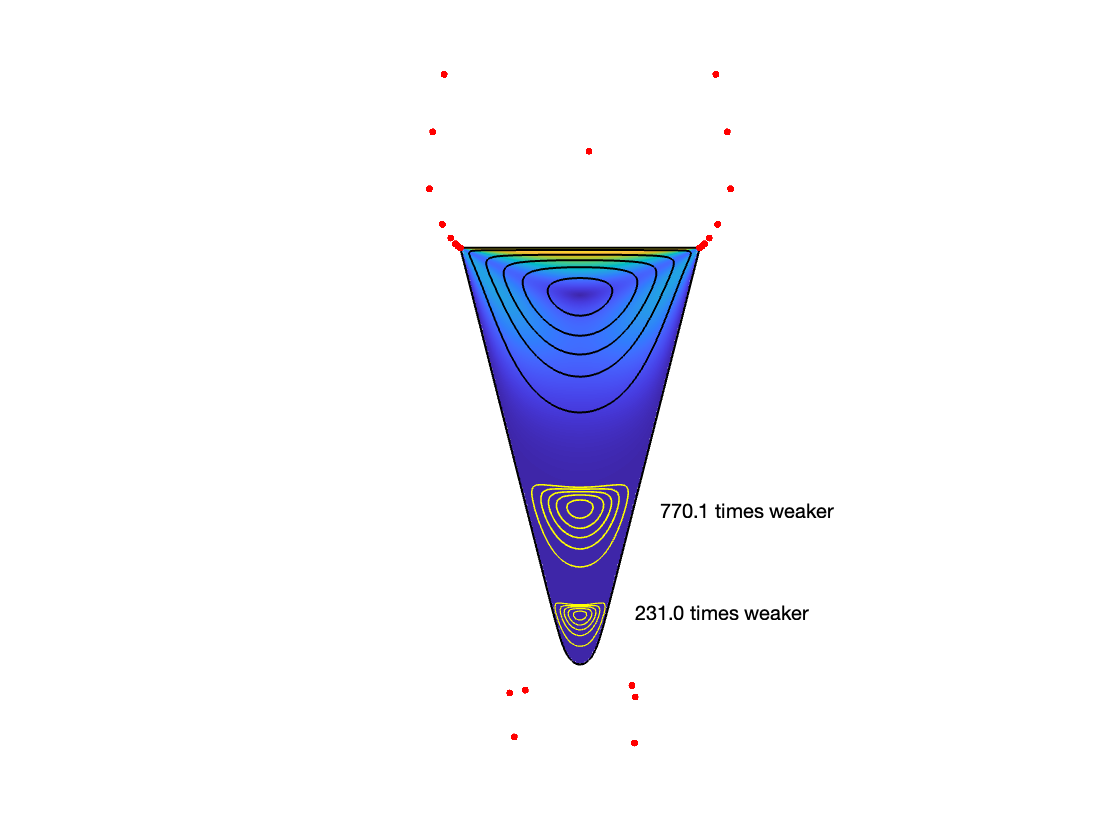 另一个demo
另一个demo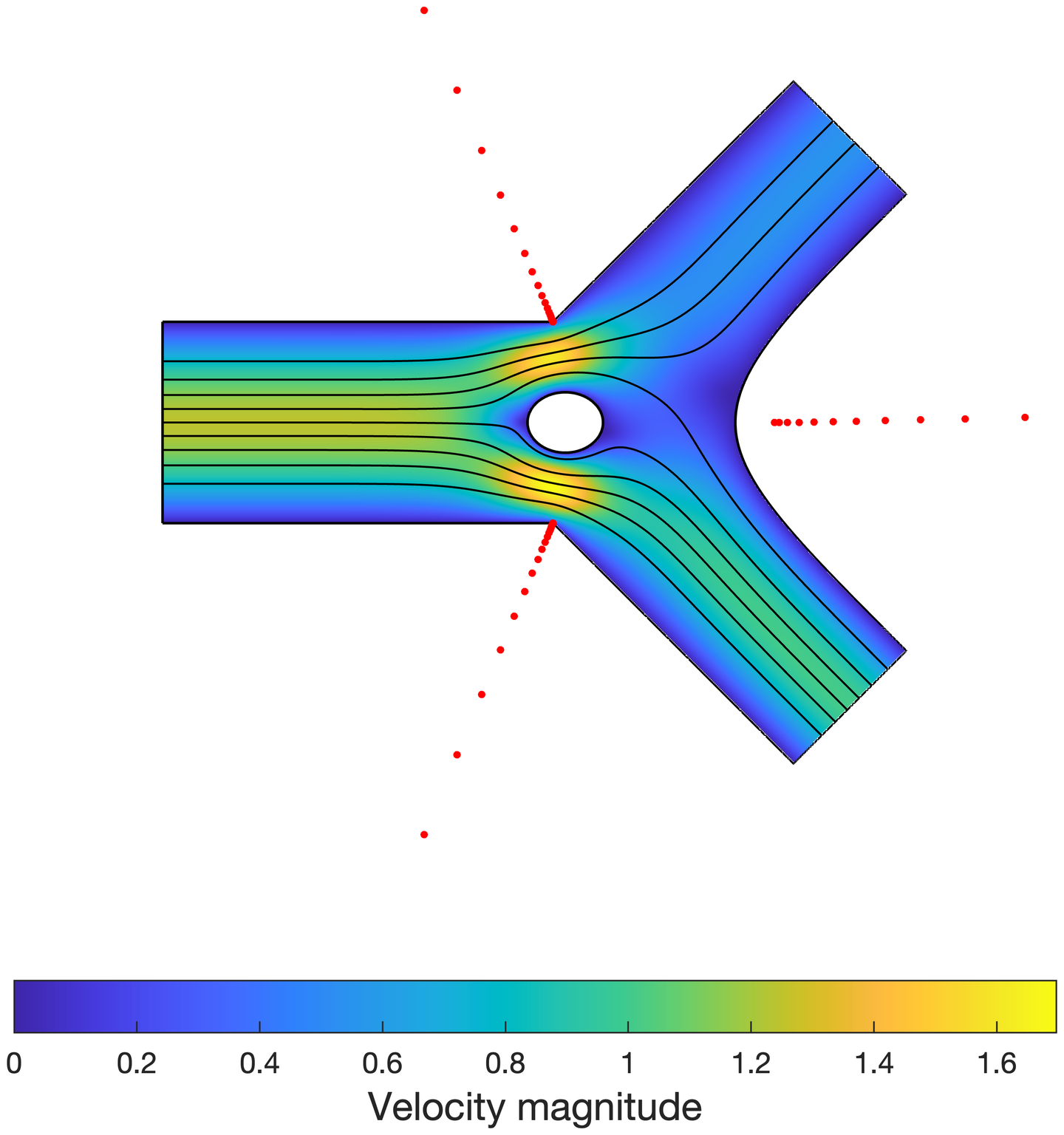 汇集了三种算法的例子(Lightning, AAA, Laurent series)
汇集了三种算法的例子(Lightning, AAA, Laurent series)